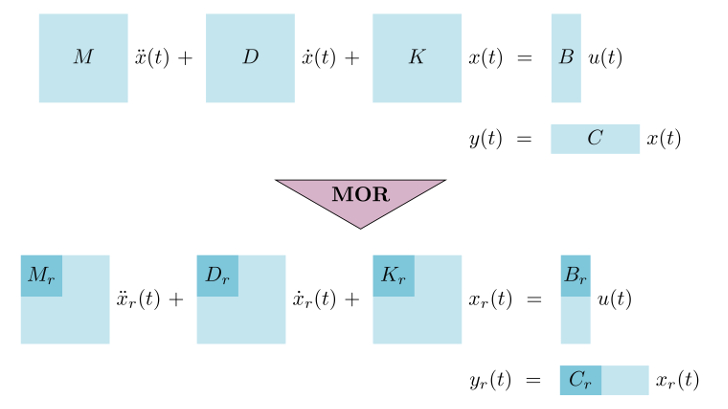
For the construction of complex mechanical structures such as bridges, buildings, or vehicles, the use of computer models is nowadays indispensable. Such computer models are typically used to simulate and, if necessary, to optimize the oscillation behavior. For instance, such an optimization is useful to suppress and damp undesired oscillations. Taking into account the input-output structure of the system, modeling of such mechanical structures typically leads to dynamical systems described by second-order ordinary differential equations.
Often the system dimension (i. e., the number of masses) is very large. The aim of model reduction is now to approximate the original system by a much smaller one to save a huge amount of computational resources during evaluation of the model.
In our project we want to develop new model reduction techniques for second-order mechanical systems that also preserve certain system properties like dissipativity.